Multisig in Bitcoin has historically involved having multiple signatures added to a transaction input. With the addition of Schnorr signatures to Bitcoin, this is no longer the case. Thanks to the linearity of the Schnorr scheme, we can combine partial signatures from multiple parties into a single signature, that's added to the transaction input. Thus, the transaction input will contain just a single signature, and a verifier won't be able to tell whether this is a normal single-signature, or a multi-signature, or something else. This saves blockchain space and increases verification efficiency, but also improves privacy, long term, as more and more users start using taproot.

In recent years, the most promising protocol for creating Schnorr multi-signatures is MuSig2 described in a paper by Jonas Nick, Tim Ruffing, and Yannick Seurin. so let's focus on that. I expect that the reader is familiar with Schnorr Signatures, which is covered in my previous post.

Multi-signature vs threshold signatures

MuSig2 is a protocol for multi-signatures, which means \(n\)-of-\(n\). To spend an output, all \(n\) signers must provide their signature. This should not be confused with threshold signatures which is a \(t\)-of-\(n\) setting that allows for any \(t\) signers among \(n\) possible signers to produce a valid signature.

The terms multisig or multi-signature have often been used in Bitcoin to refer to both threshold signatures and multi-signatures, probably because they both use the same OP_CHECKMULTISIG[VERIFY] script codes¹ to achieve them. With Taproot, however, new approaches can be used for multi-signature (i.e. MuSig2) and threshold signatures (i.e. FROST), so it becomes more important to make this distinction and use the correct terms.

MuSig2 at a glance

Suppose that Alice and Bob want to receive Bitcoin to an address that they both control together. They can do that using MuSig2 as follows

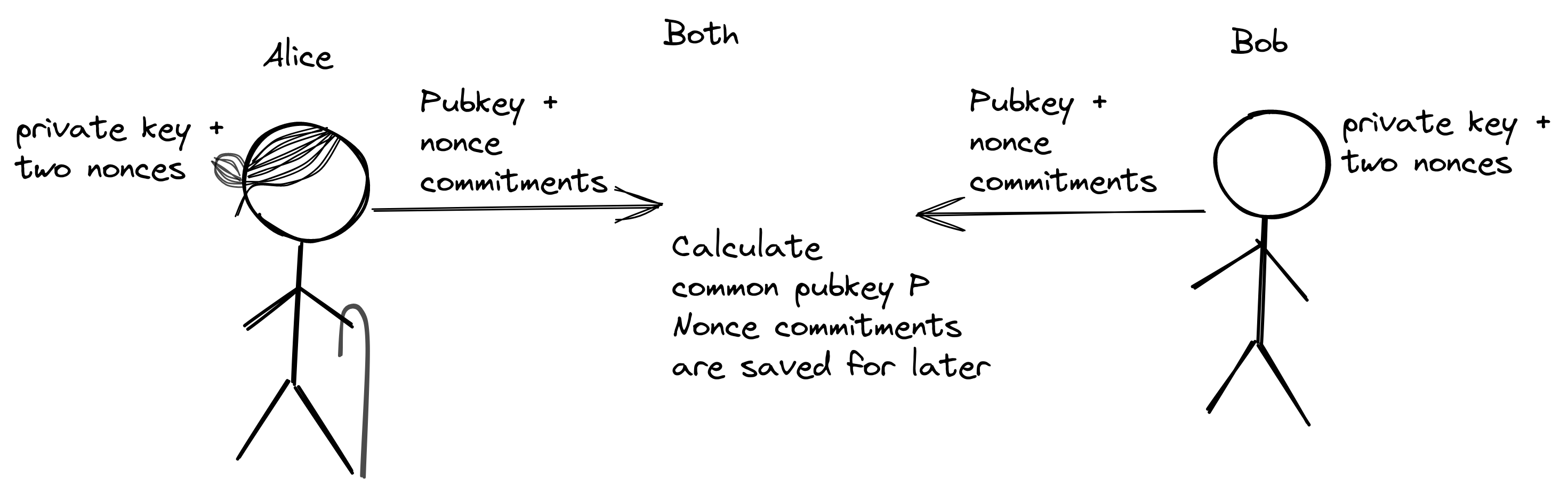
They both generate three random numbers: One private key and two nonces. They calculate the corresponding curve points for these three numbers. The result is a public key and two nonce commitments. They share these points with each other.

Using the public key data, they can now calculate a common public key \(P\) that represents both their individual public keys. This public key \(P\) is used to create a Taproot address which they can give to anyone who wants to pay to Alice and Bob. Let's say someone pays 1 BTC to this address:

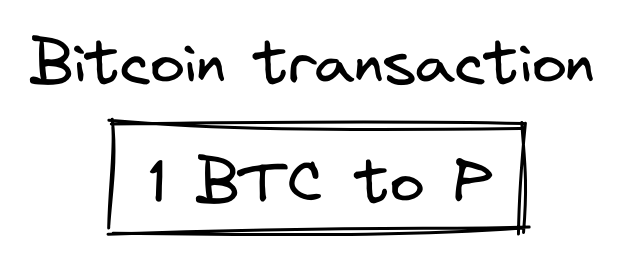
Now, suppose that Alice and Bob want to spend this output and send 1 BTC to address \(Q\). Alice or Bob would create an unsigned transaction that spends the first transaction:

Then they need to cooperate to jointly sign this transaction. The general process goes like this:

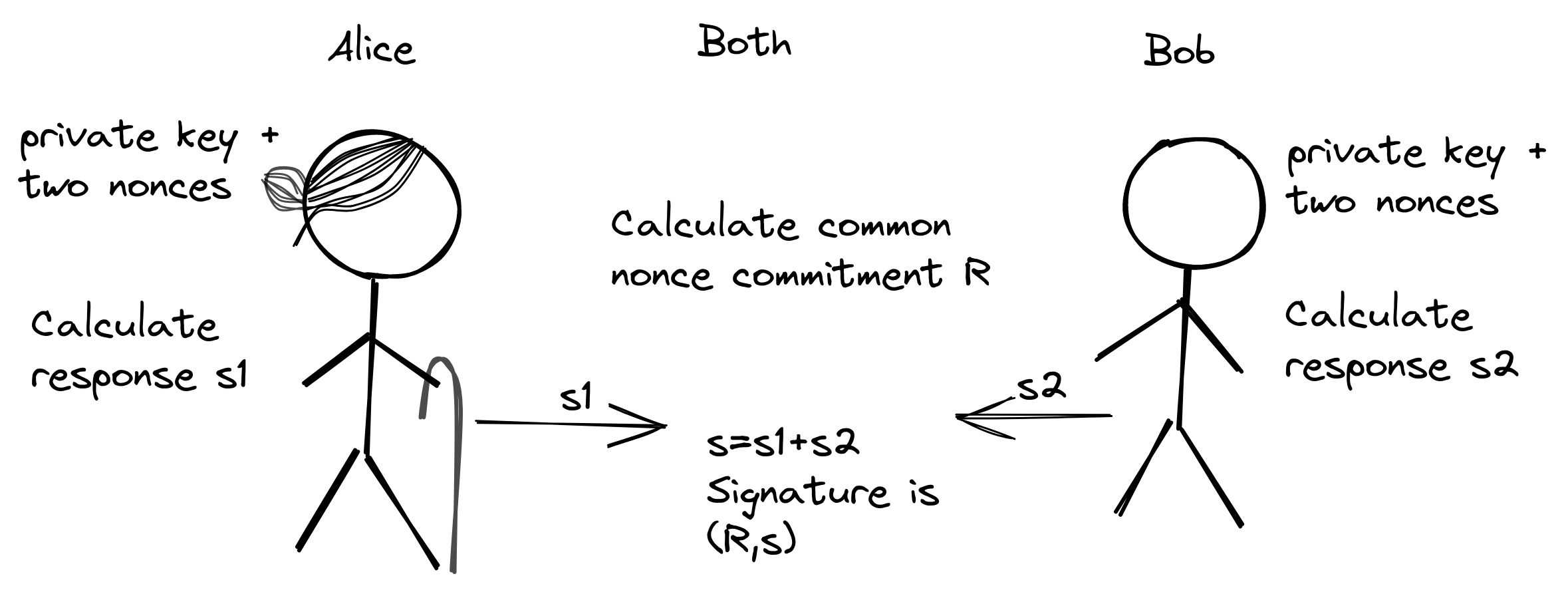
They calculate a common nonce commitment \(R\) and partial responses, \(s_1\) and \(s_2\). The final signature is then \((R,s)=(R,s_1+s_2)\)

Let's have a closer look at the two steps, public key creation and transaction signing.

Create common public key

The first step described in the overview above is the creation of a common public key from which to generate a taproot address.

Let's zoom in a bit on what Alice does (Bob does the same):

Alice has generated her own public key \(P_1\) and two nonce commitments, \(R_{1}'\) and \(R_{1}''\). She has also received the corresponding items \(P_{2}\), \(R_{2}'\), \(R_{2}''\) from Bob. She calculates the common public key \(P\) as

\[ \begin{align} &L=H(P_1||P_2) & \\ &a_i=H(L||P_i), &i=1,2 \\ &P=a_{1}P_1+a_{2}P_2 & \end{align}\]

The common public key \(P\) is a linear combination of \(P_1\) and \(P_2\). Note how each coefficient \(a_i\) (\(a_1\) and \(a_2\)) is made different² by appending \(P_i\) at the end of the hashed value. These coefficients are used to mitigate the Key Cancellation Attack, also known as Rogue Key Attack, where Alice can chose her key based on Bob's key in order to create signatures without Bob's involvement. I might write about this in a future post, but for now I suggest that you read Pieter Wuille's writings on the topic.

Even though Alice and Bob exchange nonce commitments with each other, those aren't used at this stage. They are for later, when it's time to sign a transaction. These nonce commitments are exchanged beforehand here to save one communication round later. We piggy-back the nonce commitments exchange on the public key exchange. You could, and according to some³, should, do the commitment exchange later.

Alice generates their address from⁴ \(P\) and gives it to the payer, who sends money to that address.

Sign the spending transaction

Let's look closer at how Alice and Bob cooperates to spend the output. Once again, we'll zoom in on Alice:

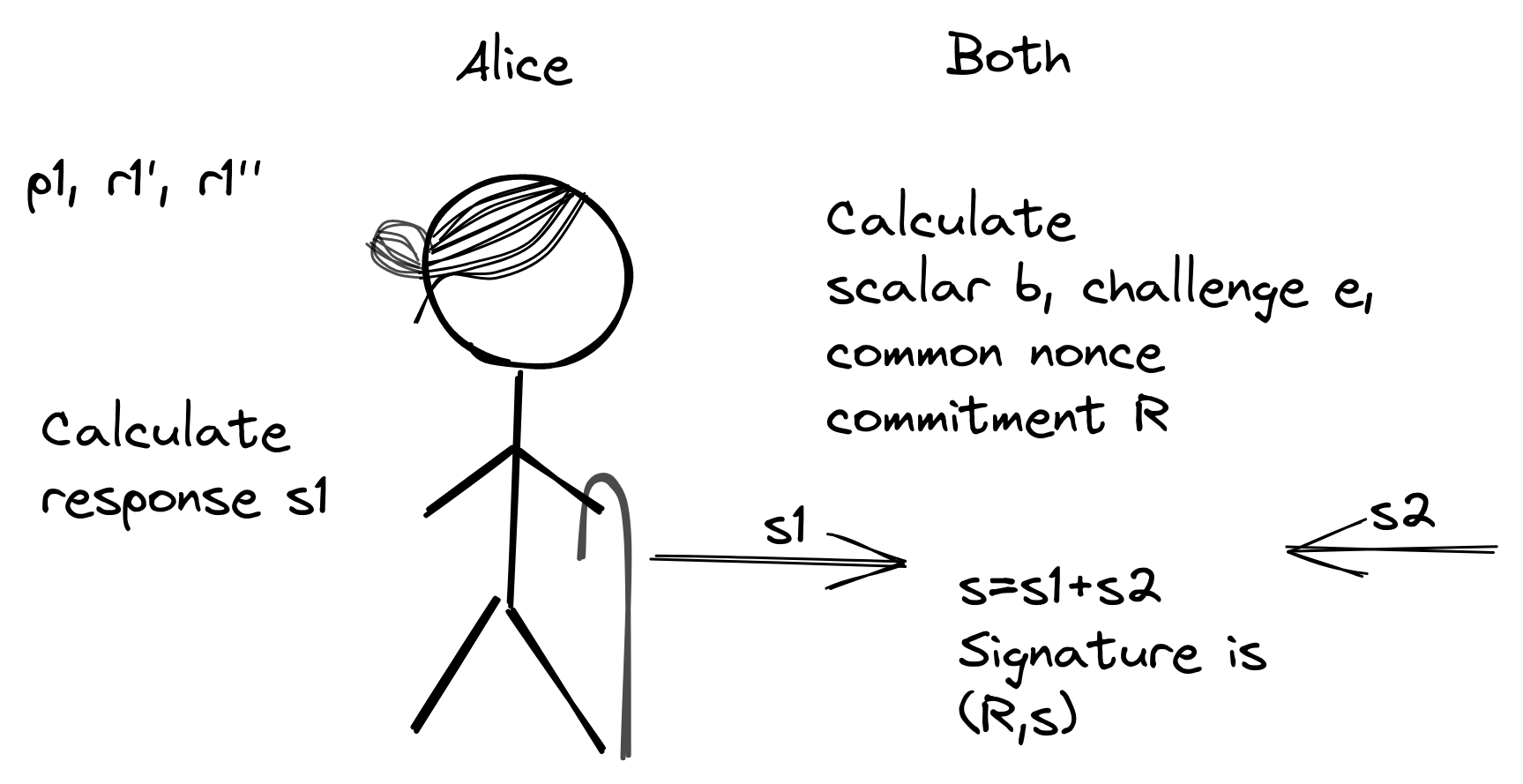
Based on all their four nonce commitments (and \(P\) and \(m\)), they both calculate a scalar \(b\), a common nonce commitment \(R\), and a challenge hash \(e\):

\[ \begin{align} &R'=R_1'+R_2' \\ &R''=R_1''+R_2'' \\ &b=H(P||R'||R''||m) \\ &R_1=R_1'+bR_1'' \tag{1} \label{ncommitment}\\ &R_2=R_2'+bR_2'' \\ &R=R_1+R_2 \\ &e=H(R||P||m) \end{align}\]

There's a lot of stuff happening here. The goal is that Alice and Bob agrees on a common nonce commitment \(R\) and can create their individual responses, \(s_1\) and \(s_2\), to finally produce a common signature. For this we need \(b\) and \(e\).

They calculate a scalar \(b\) based on both of their pairs of nonce commitments, then this scalar is used to generate a linear combination \((\ref{ncommitment})\), \(R_1=R_1'+bR_1''\), of Alice's two nonce commitments, and similarly a linear combination of Bob's two nonce commitments. These two results are then added to form the common nonce commitment, \(R\). This is the nonce commitment that'll be used in the final signature later.

Now it's time for Alice to create her response \(s_1\) (Bob will create \(s_2\) in a similar fashion):

\[ \begin{align} &r_1=r_1'+br_1'' \tag{2} \label{n}\\ &s_1=r_1+a_1ep_1 \end{align}\]

Note how Alice's final nonce, \(r_1\) \((\ref{n})\), is a linear combination of her original nonces, \(r_1'\) and \(r_1''\) and how that linear combination is a reflection of \((\ref{ncommitment})\).

Alice and Bob exchanges \(s_1\) and \(s_2\), after which both of them can construct a valid signature \((R,s)=(R,s_1+s_2)\). This signature can then be added to the witness of the transaction, which is now ready to broadcast.

Does this really work?

Alice and Bob perform a lot of weird calculations to make this signature. Let's see if the signature actually works. A verifier would use the verification equation

\[ sG=R+eP\]

so let's derive the right hand side from the left hand side:

\[ \begin{align} sG&=(s_1+s_2)G\\ &=(r_1+a_1ep_1+r_2+a_2ep_2)G\\ &=(r_1+r_2+a_1ep_1+a_2ep_2)G\\ &=(r_1'+br_1''+r_2'+br_2''+a_1ep_1+a_2ep_2)G\\ &=R_1'+bR_1''+R_2'+bR_2''+a_1eP_1+a_2eP_2\\ &=R_1+R_2+e(a_1P_1+a_2P_2)\\ &=R+eP \end{align}\]

It seems like a signature made with the correct set of private keys (\(p_1\) and \(p_2\)) is valid. But how do we know that any wrong set of private keys generates an invalid signature and that signatures can't be forged in other ways? All of this is apparently proven in the MuSig2 paper, but I can't say I even remotely understand the proofs given, so I can't verify the security of this scheme. At some point you just have to trust others.

Conclusion

MuSig2 adds some complexity compared to the legacy multi-signature implementation provided by OP_CHECKMULTISIG[VERIFY], but the improvements in verification efficiency, privacy, and transaction size should be well worth the extra effort. I think it'll take a long time before we see any actual implementations of this in Bitcoin wallets, and I'm not even sure MuSig2 will be the go-to protocol. So far there are few contestants, but maybe FROST, a protocol for threshold signatures, can be used for a multi-signature setting. I don't yet know if that's possible, but I'll find that out in a later post.

Acknowledgements

Thanks to the good people who spent their valuable time to provide feedback on this post to make it better: Ruben Somsen, Jonas Nick, and Samuel Dobson.