I've been reading the sidechains paper, and I find it really fascinating. There are a few things that I had a hard time understanding in this paper, and the Internet fell short on explaining. Therefore I'm writing this blog post to educate myself and hopefully others, as well as to validate my understanding of the paper. So please comment and correct me where I'm wrong or unclear.

Sidechains

There are several pages out there describing the overall idea of sidechains, so I won't write about that here. Instead I suggest the following pages:

• Sidechains paper
• http://www.coindesk.com/sidechains-white-paper-ecosystem-reboot/
• https://gendal.me/2014/10/26/a-simple-explanation-of-bitcoin-sidechains/

The basic idea is that you lock an amount of coins on one blockchain, A, that you later can claim on another blockchain, B, if the corresponding amount is previously locked on B. To unlock the funds on A again, you need to first lock a corresponding amount on B, and provide an "SPV proof", proving that such a locked output exists. The following image illustrates this process:

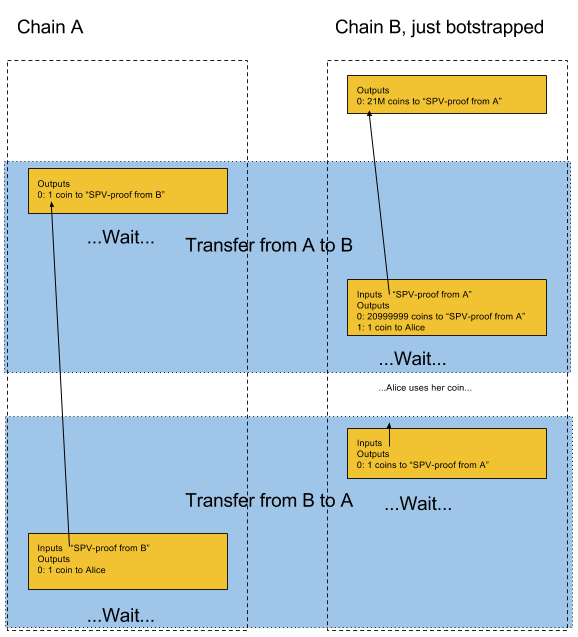
This blog post will describe how SPV proofs work and how a reorganisation proof can block the transfer from happening, if the block containg the locking output gets stale.

From the paper, an important property of sidechains is that a chain A doesn't have to follow another chain. For example, the Bitcoin clients should not have to keep track of every single sidechain in order to verify Bitcoin transactions transferring funds from other chains. It really helps keeping this in mind while reading about sidechains.

SPV proofs

When the parent chain locks funds it encumbers them with a rule saying

In order to spend these funds you must provide a proof that an SPV-locked output on the sidechain B exists and that enough PoW has been generated on top if it. You must also prove that you actually own the coins on sidechain B.

So when funds are moved back from the sidechain to the parent chain, meaning you spend the previously SPV-locked parent chain funds, you need to construct a proof satisfying the rule above. This first part of the proof is called an "SPV proof", from Simplified Payment Verification as described in the Satoshi whitepaper. This is what an SPV proof looks like:

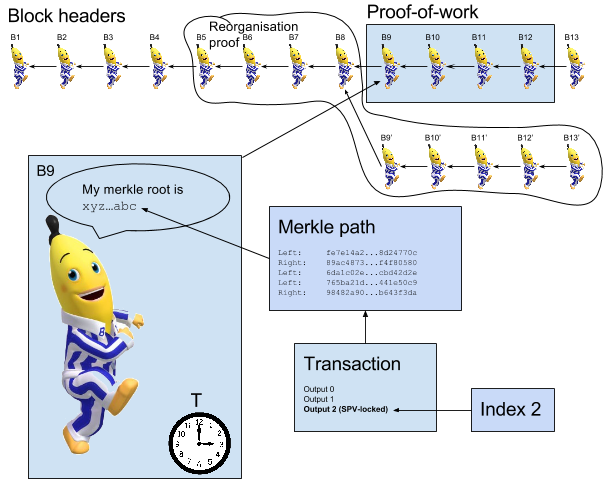
The proof contains:

1. The blockheader of the block containing the SPV-locked output.
2. A list of connected block headers following directly after the block in 1. This list and 1 functions as proof-of-work.
3. The transaction containing the SPV-locked output
4. The index of the SPV-locked output within the transaction in 3.
5. A merkle path proving that the block in 1 actually contains the transaction in 3.

In section 3.2 of the paper it reads "a special output on the parent chain that can only be unlocked by an SPV proof of possession on the sidechain", It means that apart from the SPV proof itself the receiving transaction must also provide proof of possession of the funds. This is the second part of the rule above. That's important, because without it, anyone can take the funds on the receiving chain. How the proof of possession is achieved is a bit unclear in the paper, but BIP120 (Proof of Payment) comes to mind, where you can prove that a certain transaction was in fact created by you. You can simply attach a PoP and its parent transactions to the SPV proof and you're done.

Reorganisation proofs

What if a reorganization happens on the sending side of the transfer? Did you notice the waiting periods in the first picture? The first waiting period in a transfer is called the "confirmation period". This period is the time you have to wait before even being able to construct an SPV proof, because of the "and that enough PoW has been generated on top if it" part of the output you're trying to spend.

The second waiting period is on the recipient side of the transfer, and is called "contest period". If a reorg happens on the parent chain during the contest period, then the transfer is "retroactively invalidated" as it says in the paper. I don't know what that actually means. Please leave a comment if you know what it means. See next section for some elaboration on this.

Anyway, a reorg proof is a sequence of block headers that prove that more work has been made on a branch NOT containing the block containing the SPV-locked output:

In the picture, B9 is not included in the list of blocks, because there is an alternate blockchain containing B5-B8 and B9'-B16'. The proof is quite big because, as I understand it, the proof needs to include ALL blocks on the alternate chain where B9 could possibly be located. In this case it means all blocks from time T-4h to T+4h. That's because a timestamp is only accurate within roughly 2h. In the example, B5 needs to have a timestamp of <T-4h to make sure that B9 is not before B5 in the chain. Similarly, B13' needs to have a timestamp >T+4h to make sure B9 is not after B13'. Then on top of that we need to provide PoW from the time after and including B13' to prove that enough work has been committed to this "lacking B9 chain".

Reorg proofs using covenants

How can the sidechain clients know if a reorg happens on the parent chain without following the chain?

The answer seems to be that it's up to the participants of the sidechain to keep track of that. One way of solving this could be to use Bitcoin Covenants, where an output puts restrictions on the transaction spending the output. For example

This output is spendable by a signature from Alice after X blocks OR by a reorg proof within X blocks from this transaction with the covenant that the output of the spending transaction must be SPV-locked.

This means that any party can, within X blocks, spend the output using a reorg proof and send the money back to an SPV-locked output, effectively undoing the redeeming transaction. This is of course dependent on reorg proofs being compact enough to fit in a transaction.

Please write in the comments if you find any errors here. I just came up with the idea and thought I'd throw it out here.

Height based reorg proofs

Reorg proofs could be made smaller if blocks committed to their height. This commitment be done for example by an explicit height number in the coinbase transaction, or as part of the segregated witness merkle root in the coinbase transaction, which is usable for other purposes than just segregated witness. Then a reorg proof would look something like this:

Now the competing B9' is the only header needed to prove that there is another chain where B9 is not present. And on top of that you need the proof-of-work to show that more work has been committed to B9' than to B9.

What's next?

In the next couple of blog posts, I'll write about compact SPV proofs (possibly applicable to reorg proofs as well), atomic swaps and possibly other nice topics related to sidechains.