This is a follow-up post on my series on sidechains. I recommend reading SPV proofs and reorg proofs in sidechains and Compact SPV proofs in order to understand this post. But if you're already familiar with sidechains, just go ahead!
There is a risk that miners collude to steal sidechained coins. I know of at least two ways that's possible.
Create a real SPV-locked output then reorg
One way is to cause a reorg on the sending chain, like an ordinary double spend attack. You are a gangster and as soon as you find a block, you withhold it and start working on a hidden chain. At the same time you publish an SPV-locked output to the honest network who will include it in its next block. While the honest network is busy committing work to your output, you keep on building your private chain.
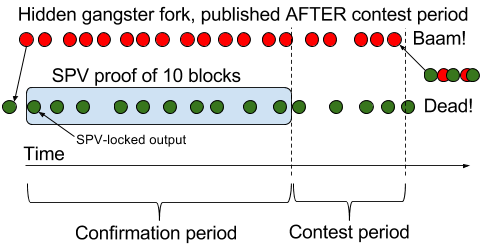
When you can prove enough work on the honest chain, you create an SPV proof and publish a receiving transaction on the recipient chain. Then you continue to work on the hidden chain and when the contest period is over, you publish your hidden chain. If you have 51% of the sidechain's hash power, this is a given. The risk for you is nearly zero. This attack is no different from a normal double spend attack, other than in this case money is stolen collectively from other people instead of double spending one's own money. The attacker needs to temporarily commit Y coins of her own money on the sidechain in order to steal Y coins on the main chain, so she can't steal more money than she has. But the process can be repeated over and over, doubling her money in each iteration.
What happens to the confirmation period and the contest period when about half of the hashing power works on a hidden chain?
The confirmation period is (probably) expressed in number of sidechain blocks This means that the SPV-locked output must be buried under that number of blocks before the receiving transaction can be created. So the confirmation period will roughly double in time.
The contest period cannot be expressed in sidechain blocks, since the main chain doesn't follow the sidechain; It must be able to determine when the redeemed coins are spendable without having to follow the sidechain. So it's either expressed in time or in number of main chain blocks. The contest period will thus not be affected by the hidden hash power.
The paper states in section "4.2 Fraudulent transfers":
the risk [of theft] can be made arbitrarily small by simply increasing the contest period for transfers.
While this is true for an attacker with < 50% it doesn't hold for a 51% attack.
It should be possible to detect a 51% attack by looking at the time it took to produce the SPV proof, for example by comparing to other SPV proofs from before, and if the proof spans a significantly, say 95%, longer time period, refuse the SPV proof. This would open up for denial-of-service attacks where a big miner on the sidechain can block ALL transfers from the sidechain. We would also run into similar problems if a sudden drop in hash power occurs naturally. Can you think of more ways to detect/mitigate this attack?
One should also be aware that increasing the contest period also opens up for DOS-attacks; Say that the contest period is 10 times the confirmation period, then a miner with 10% hash power will be able to fake a reorg proof during the contest period, effectively blocking the transfer from happening.
Since there is little to no risk for the attacker, I can very well envision a group of mining pools collude to do this, but it won't go unnoticed. When it becomes apparent that money has been stolen, the money that were still on the sidechain would quickly be withdrawn back to the main chain by everyone, and the unfortunate last people doing it would fail because there are no SPV-locked outputs left on the main chain to claim. They would probably not be socially powerful enough to enforce a hardfork to get their coins back. The end result is that the main chain is technically unaffected, and nobody will trust the sidechain, which will die, leaving the unfortunate ones ruined.
If the attacker is smart she'll probably add a double-spending SPV-locked output on the hidden chain with all her sidechain coins, so that they are ready for transfer as soon as the reorg happens. She doesn't want to risk her coins being stuck on the sidechain due to the "no outputs left on main chain" issue that she'll cause.
One should also mention that she'll be giving up her sidechain's native block rewards (if there are any) of the sidechain. With giving up, I mean that the native tokens will probably be worthless once she has pulled this off.
Create a fake SPV-locked output
Another way to steal coins is to create a fake SPV-locked output on the sidechain, spending non-existent money, and create an SPV proof on top on that output. They have 51% of the sidechain's hash power, and start their attack on block height X. Say that the proof needs to prove 10 blocks worth of work (I know, it's unrealistically small, but the picture becomes simpler). At the time they're finished with their proof and created their redeem tx, the honest chain might have produced about 8 blocks starting in an "honest block" at height X. So just 3 blocks into the contest period a reorg proof can be created and invalidate the redeem tx.
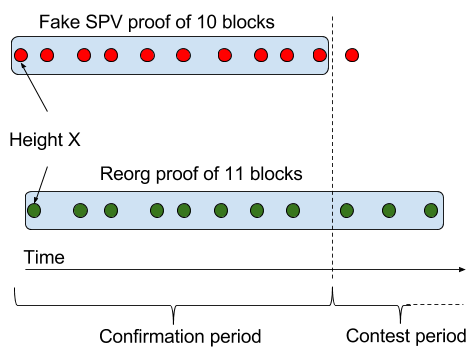
One should note that an SPV proof proving more than the required amount of work is not going to increase their chances, because the validation rules should only check if enough work is proven. This means that 51% is not enough to steal coins this way.
How much would be needed then? Assuming the contest period is equally long as the confirmation period, 2/3=67% of the hashing period should be enough. Then when the fake proof is finished, the honest chain has only produced around 5 blocks, and will probably not be able to produce another 6 blocks during the contest period.
This vector is further disincentivized by the fact that you get no sidechain rewards for the work performed on the fake SPV proof.
Conclusion
Theft of sidechained coins in a 51% attack on the sidechain is a real threat. There doesn't seem to be any good solution to it, apart from some heuristics on the timespan of the SPV proofs, which opens up for some DOS-vectors. I'm interested in hearing your thoughts on this issue. Please comment below or on reddit.
P.S. It's really time for me to fully read and understand Paul Sztorc's drivechains. His general idea is to acknowledge this 51% attack problem and let miners vote on coin transfers, since they have this power anyway, saving us from the cumbersome SPV proofs.
